Como dijimos, la modelización de un problema a través del álgebra es una tarea compleja, que no se reduce a una simple interpretación de un enunciado. Requiere entenderlo, poder extraer de él sus datos relevantes, darse cuenta cuál es la pregunta que se está haciendo, buscar algún tipo de relación entre los datos y finalmente escribir la o las ecuaciones que modelizan el problema. Luego de este proceso se está en condiciones de intentar resolverlo. En esta resolución también aparecen inconvenientes, ya que los alumnos replican algoritmos memorizados que hacen surgir errores difíciles de desarraigar.
Todos los documentos curriculares vigentes destacan la importancia de capacitar a los estudiantes en una introducción al Álgebra de modo tal que los ayude al reconocimiento, uso y análisis de expresiones algebraicas y variaciones, funcionales o no, en sus diferentes representaciones y en situaciones diversas.
La aproximación al Álgebra que se propone es partir de problemas y resolverlos poniendo en acto el procedimiento algebraico que implica pasar del enunciado verbal a la puesta en ecuación. Este paso de la lengua natural al lenguaje algebraico es precisamente la escritura de ecuaciones que aparecen entonces como un medio adecuado para la resolución de problemas y el cálculo literal como el medio para accionar en la búsqueda de las soluciones.
La resolución de las ecuaciones necesita del conocimiento de un cierto número de reglas de cálculo literal que los alumnos construyen a medida que analizan las situaciones que se les presentan. Apropiarse paulatinamente del lenguaje del Álgebra implica, por ejemplo, dejar de considerar al signo “=” como una señal para realizar alguna operación e interpretarlo como un indicador de equivalencia. Es un proceso que lleva tiempo y no se alcanza en un año de estudio sino que se va consolidando a medida que el alumno llega a la comprensión de lo que representan los símbolos y cómo se manejan las operaciones algebraicas. Si bien los alumnos han utilizado antes en la aritmética la mayoría de los símbolos del Álgebra, ampliar su nuevo significado no se logra de un día para otro.
En muchas ocasiones, en la escuela se inicia a los alumnos en los conceptos de ecuación y solución de una ecuación mediante definiciones formales. Muchos libros de texto también eligen este camino. Sin embargo, también se observa en muchos casos un reiterado fracaso en el aprendizaje.
Esta observación conduce a pensar en la necesidad de buscar otros caminos en la enseñanza para que los alumnos se aproximen al tratamiento algebraico de los problemas. Las publicaciones de los investigadores y las experiencias de otros colegas dan fundamento a esta propuesta con relación a la enseñanza del Álgebra.
A continuación se proponen actividades (seleccionadas del Cuaderno de estudio 2: Matemática. Ministerio de Educación Ciencia y Tecnología de la Nación. 2007. ISBN 978-950-00-0649-1), que no se constituyen en una secuencia de enseñanza, sino pautas para el trabajo en el aula.
Las figuritas
Leé la siguiente situación y luego respondé las preguntas que hay intercaladas en el relato.
Paula y Mariana coleccionan figuritas. Martín le preguntó a Paula cuántas figuritas tenía. La respuesta de Paula fue: “Con 6 más voy a tener cuatro veces lo que tiene Mariana”. Martín pensó un rato y razonó así: Si Paula tiene 2 figuritas, con 6 más son 8 y entonces Mariana tiene 2 figuritas. Pero si Mariana tuviera 5, Paula debería tener 14 figuritas.
- ¿Es correcto el razonamiento de Martín?
- Expresá con símbolos esa situación.
- Comprobalo y escribí otro par de números que puedan dar solución al problema.
Martín resolvió hablar con Mariana, pero, para no olvidarse, y pensando que p es el número de figuritas de Paula y m el número de figuritas de Mariana, anotó: p + 6 = 4 . m. Cuando se encontraron Mariana le dijo que tenía 10 figuritas. Miguel, que no sabía cuál era el problema, vio escrita la igualdad de Martín y pensó: “Si en lugar de p se pone 6, también hay que cambiar m, y para que la igualdad se cumpla, hay que poner 3”.
- ¿Cuántas figuritas tiene, entonces, Paula?
- Ensayá otra sustitución de p y averiguá cuál es la sustitución de m que corresponde para que la igualdad: p + 6 = 4 . m sea verdadera.
-
¿Se puede poner cualquier número en lugar de p? Hacé una tabla y explorá distintos valores de p y m.
- Los números que hacen verdadera la igualdad tienen una característica común; ¿cuál es?
Proceso de generalización
Respondé en tu carpeta las siguientes preguntas.
-
¿Cuál es el área de un rectángulo de 3 m (metros) de base y 5 m (metros) de altura?; ¿y la de uno de 4 m por 6 m?; ¿y la de uno de 5 m por 7 m?; ¿y la de uno de lados de 8 m y 10 m?
-
La colección de rectángulos anterior tiene una característica común que es la relación entre sus lados a y b. Escribí simbólicamente esa relación.
-
Ahora dibujá uno de esos rectángulos y usá b como lado para dibujar un cuadrado dentro del rectángulo. Describí las dos figuras en las que ha quedado dividido el rectángulo.
-
Escribí el área de cada rectángulo expresada como la suma del área del cuadrado más el área de la otra figura.
-
Si llamás x a la base del rectángulo, ¿qué fórmula permite calcular el área total teniendo como único dato la medida x de la base? Esa fórmula ¿es válida para cualquier rectángulo de esta familia?
-
¿Pensás que la fórmula que hallaste tiene una única expresión simbólica? Comparala con la de otro compañero y consultá con tu docente sobre los resultados.
Expresiones algebraicas equivalentes
- De la siguiente lista de ecuaciones, determiná cuáles son equivalentes a
20 + x = 25.
1. 25 – x =20
2. 18 + x = 23
3. x – 2 = 7
4. x = 25 – 20
5. 25 + x = 20
6. 20 + x – 25= 0
7. 20 x = 25
8.
9. 2 x + 15 = 25
10. 20 + x = 15
- Si en la consigna anterior contestaste que algunas son equivalentes a la ecuación propuesta, respondé:
- ¿Qué transformaciones se hicieron en 20 + x = 25 para llegar a ellas?
- Escribí los ejemplos y cómo los resolviste.
Para resolver con ayuda del Álgebra
- En dos sectores de una estantería hay guardados autos de juguete. Todos los autos son iguales.
El sector izquierdo de la estantería mide lo mismo que el derecho.

- Expresá con símbolos esta situación.
- Calculá, empleando la ecuación que escribiste, cuánto mide cada auto.
- ¿Cuál es el largo de cada sector de la estantería?
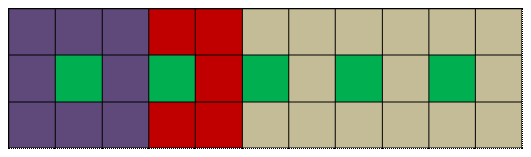
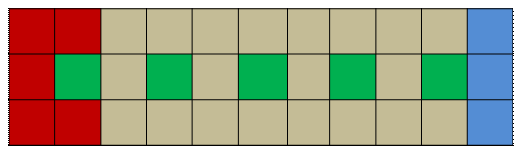
- Un comercio vende alfajores en cajas de distinto tamaño. Cada caja contiene los alfajores de dulce de leche envueltos con papel dorado, y los de fruta, con papel plateado, según lo muestran las tres cajas rectangulares que ves en la figura de abajo, siempre con tres filas en cada una.

- ¿Cómo podés expresar la relación entre la cantidad de alfajores de una y otra clase que hay en cada caja?
- Si sabés cuántos alfajores de dulce de leche hay en una caja, ¿podés decir cuántos hay de fruta y cuántos en la totalidad de la caja?
- Si sabés que una caja tiene 36 alfajores en total, ¿podés averiguar cuántos de cada clase contiene?
Cálculos mágicos
a) A continuación vas a leer una situación que describe un juego realizado en un aula entre los alumnos y su maestro. Está presentada en dos etapas. Resolvé las consignas de cada etapa, y así podrás desarrollar el juego en tu aula. Probalo con algún compañero de otro año. Acordá con tus compañeros de año para que todos puedan probar el juego con diferentes personas.
-
Aníbal le propuso a otro compañero que piense un número menor que 50 y lo escriba en un papelito sin mostrárselo a él porque lo iba a adivinar. Le dio las siguientes órdenes para que hiciera cálculos mentales sin decir los resultados hasta que él se lo indicara:
• Sumale 10.
• Multiplicá por 3.
• Restá 6.
• Dividí por 3.
• Restá 6.
• Ahora decime, ¿qué número te dio?
Aníbal le restó 2 a ese número y, en efecto, acertó. - El maestro pidió a los chicos que explicaran el truco, y Aurora lo hizo por escrito, escribiendo ecuaciones:

• Copiá en tu carpeta la explicación de Aurora, analizála y respondé, ¿es correcta?, ¿por qué?
- Con algún compañero, repitan el truco entre ustedes eligiendo otros números para las instrucciones y escriban en ecuaciones el procedimiento para llegar a la solución.
¿Todas las expresiones algebraicas son ecuaciones?
Muchas veces trabajás con enunciados o con igualdades en las que intervienen letras, pero eso no es suficiente para que sean ecuaciones. Copiá las siguientes expresiones o enunciados, analizalos y decidí cuáles son ecuaciones. Explicá por qué.
• 2 (3x + 4y)
• 5 (3b – 2) = 7(b + 2)
• La suma de un número con su mitad es 15.
• 12a +15a – r
• Un número y su cuarta parte.
• Tengo 87 pesos y lo gasto todo menos 17. ¿Cuántos me quedan?
• La base de un rectángulo es 5 cm mayor que su altura y su perímetro es 36 cm.
• Un bolígrafo cuesta 2 pesos más que un lápiz.
• x =
• 13 + 7 = 20
• 2 (z – 1) = 0
• a + b = b + a
b) ¿Qué podés decir acerca de las expresiones anteriores que no son ecuaciones?
Una entrada al álgebra
La siguiente actividad está presentada con fases para la presentación en el aula y con un análisis de las posibles respuestas de los alumnos. La intención es “poner en fórmulas” una relación entre variables, es decir realizar un pasaje de una formulación escrita a una fórmula matemática. Las características que tiene son: el soporte es familiar y permite la validación geométrica de sus soluciones; el problema permite utilizar diferentes métodos de cálculo y obtener diferentes fórmulas para el cálculo de cuadrados sombreados y todos los alumnos son capaces de producir algún tipo de respuesta, las diferentes respuestas dependen del nivel de generalización de las formulaciones.
Establecer una fórmula que permita calcular el número de cuadrados sombreados de una figura construida sobre el modelo que a continuación se muestra, conociendo el número de cuadrados sobre el borde del cuadrado original. Suponga que es de lado 5 cuadraditos.

¿Cómo se puede presentar a los alumnos?
Primera fase:
Primera etapa: cálculo de cuadrados sombreados en la figura dada de 5 cuadrados de lado, responden rápidamente y comentan los resultados obtenidos y cómo lo hicieron.
Segunda etapa: transposición de un problema a una figura difícilmente de dibujar, por ejemplo calcular los cuadrados sombreados de un cuadrado de 37 cuadraditos de lado
Los procedimientos que los alumnos pueden utilizar son los siguientes
- 37+36+36+35

- (37×37)-(35×35)

- 36×4

- 37×4-4

- 37+37+35+35

- 37×2+35×2
Segunda fase:
En grupo, los alumnos formulan un método de cálculo explicando con palabras lo obtenido –en una o más frases–, pero para el cuadrado de lado 37, no se pide un procedimiento general de cálculo.
Ejemplo: se multiplica por cuatro el número de cuadraditos que hay en el lado del cuadrado. Luego se retiran cuatro cuadrados del resultado y se obtiene el número de cuadrados sombreados.
Tercera fase:
Puesta en evidencia de diferentes procedimientos de cálculo
Las formulaciones producidas son expuestas, entonces se eliminan los métodos que no permiten calcular el número de cuadrados sombreados justificando por qué. El docente reagrupa las formulaciones que correspondan a un mismo método de cálculo. Permite la confirmación de métodos y la reformulación de otros.
Cuarta fase:
Pasaje de una formulación a una fórmula. Se quiere pasar de una formulación escrita a una escritura matemática en donde el número de cuadrados que hay en el lado es designado por una letra.
El docente propone escribir un cálculo que permita obtener el número de cuadrados sombreados que sirva para todos los cuadrados. Le solicita a sus alumnos que expliquen los símbolos y letras que utilizan
La puesta en común de fórmulas tiene por objetivo poner en evidencia lo siguiente:
- una letra reemplaza cualquier valor numérico, no importa cuál;
- las escrituras propuestas por los alumnos como diferentes, por las letras que emplea, se reconocen como idénticas y corresponden a un mismo método de cálculo;
- las fórmulas escritas, en todas las etapas diferentes son equivalentes, y si se reemplaza por un mismo número, en cualquiera de ellas, se obtiene el mismo resultado.
Sucesión de figuras con fósforos:
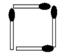
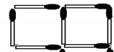

Tareas:
- Calcular la cantidad necesaria de fósforos para construir la figura que ocuparía el sexto lugar.
- Calcular la cantidad necesaria de fósforos para construir la figura en el lugar 100 de la secuencia.
- Si tengo 1550 fósforos y armo una figura de esta forma lo más grande posible ¿me sobra alguno?
- Hallar la fórmula para la cantidad de fósforos del lugar “n”.
Otro para terminar…..
“Para separar un patio de un lavadero se colocan, en línea, canteros cuadrados rodeados de baldosas de la misma forma”
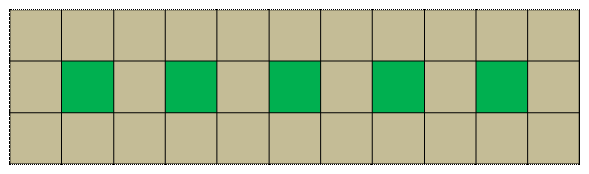
Si se colocan 4 canteros, ¿cuántas baldosas se requieren para rodearlos?
¿Y si se colocan 6? ¿y 100?
Al resolverlo los alumnos, dependiendo de la forma de contar, pueden lograr las siguientes fórmulas:
8+5.(n-1)
5.n+3
Y así se podrán arribar a otras como:
3.(n+1)+ 2 n
3.(2n+1)-n
2.(2n+1)+n+1
Es decir:
- De un mismo problema, se obtuvieron más de una expresión para la generalización.
- La letra “n” representa una cantidad variable perteneciente a un dominio natural.
- Todas las expresiones son EQUIVALENTES.