Los errores recurrentes evidenciados en nuestros alumnos por el bajo porcentaje de respuestas correctas en el bloque de “Operaciones” tienen sus causas en varios factores, uno de ellos es la incorporación de un nuevo conjunto numérico, el conjunto de los números racionales y por otro lado la incorporación sistemática del análisis de variaciones funcionales, lo que hace que los alumnos tengan que reconocer y utilizar relaciones directa e inversamente proporcionales.
Es importante remarcar que la incorporación de los números decimales y las fracciones en el segundo ciclo, implica un nuevo trabajo en la tarea docente, con la consabida complejidad que representa el aprendizaje de estos conjuntos numéricos.
Cálculos mentales con fracciones
En esta secuencia de problemas se propone que los alumnos realicen cálculos que les permitan progresar en el conjunto de relaciones que se establecen entre determinados grupos de fracciones y entre ciertas fracciones y los enteros.
¿Qué se entiende por cálculo mental? El cálculo mental se asociaba tradicionalmente a cálculos memorizados o también a cálculos realizados “en la cabeza”, sin apoyo de lápiz ni papel. No es en este sentido que lo estamos caracterizando.
Entendemos por cálculo mental los procedimientos de cálculo que se oponen a los cálculos algoritmizados (serie de reglas aplicables en un orden determinado, siempre del mismo modo independiente de los datos que están en juego). El cálculo mental considera la construcción de procedimientos personales que permiten dar respuesta a una situación. En el cálculo mental, a partir de un resultado conocido o de fácil obtención, se despliegan diversos procedimientos basados en las propiedades de las operaciones (aunque éstas no siempre se expliciten).
Por ejemplo, en uno de las siguientes tareas se pregunta cuánto le falta a ![]() para llegar a dos enteros. Un criterio algoritmizado del cálculo supone que para responder a esta situación sería necesario plantear la resta
para llegar a dos enteros. Un criterio algoritmizado del cálculo supone que para responder a esta situación sería necesario plantear la resta ![]() y luego considerar los pasos para efectuar una diferencia entre un número natural y una fracción. Sin embargo, se espera que los alumnos lleguen a obtener las respuestas por diversos caminos, basados en sus conocimientos, ya que el problema se propone en un momento en el que la resta no fue aún formalizada.
y luego considerar los pasos para efectuar una diferencia entre un número natural y una fracción. Sin embargo, se espera que los alumnos lleguen a obtener las respuestas por diversos caminos, basados en sus conocimientos, ya que el problema se propone en un momento en el que la resta no fue aún formalizada.
- ¿Cuáles de las siguientes fracciones son mayores que un entero? Explicá cómo lo pensaste.
![]()
- ¿Cuánto les falta para llegar a 1?
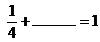
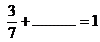
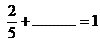
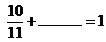
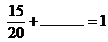
- ¿Cuánto les falta para llegar a 2?
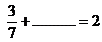
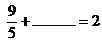
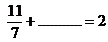
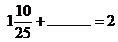
- Completá la tabla:
|
Fracción |
Mitad |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- Para discutir:
En relación con el ejercicio anterior, Nicolás opina que si ![]() es la mitad de una fracción, entonces la fracción es
es la mitad de una fracción, entonces la fracción es ![]() . En cambio, Laura opina que es
. En cambio, Laura opina que es ![]() . ¿Vos qué opinás? ¿Quién tiene razón?
. ¿Vos qué opinás? ¿Quién tiene razón?
Fracción de una cantidad
Esta serie de problemas apuntan a realizar tareas en donde las fracciones no hacen referencia a una parte de un objeto sino a una parte de una colección formada por más de un objeto.
Esto da lugar a que se pueda pensar el problema en función de dos unidades de medida: puede considerarse como unidad cada objeto de la colección o el total de objetos.
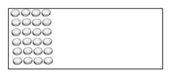
- Una panadería recibe, para vender, una bandeja con alfajorcitos de dulce de leche. Si están representados
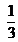 de los alfajorcitos porque el resto ya se vendió:
de los alfajorcitos porque el resto ya se vendió:
a. ¿Cuántos alfajorcitos se vendieron?
b. ¿Cuántos alfajorcitos traía la bandeja?
- Se sabe que
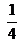 de los globos son rojos. ¿Cuántos deben pintarse de ese color para que la afirmación sea correcta?
de los globos son rojos. ¿Cuántos deben pintarse de ese color para que la afirmación sea correcta?

- Este pilón de monedas es sólo
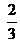 de los ahorros de Martín. ¿Es posible saber cuántas monedas tiene ahorradas en total?
de los ahorros de Martín. ¿Es posible saber cuántas monedas tiene ahorradas en total?

- De todas las bolitas que Pablo tenía, perdió
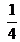 . En la ilustración pueden verse las que le quedaron. Dibujá cómo era la colección completa de bolitas.
. En la ilustración pueden verse las que le quedaron. Dibujá cómo era la colección completa de bolitas.

La construcción del campo conceptual de la proporcionalidad directa
Estamos acostumbrados a pensar en la proporcionalidad como un contenido escolar que se trabaja en un determinado momento, se desarrolla, se ejercita, y se da por finalizado para pasar al tema siguiente, que podrá ser fracciones, medida, decimales, geometría o cualquier otro que figure entre los contenidos que debemos desarrollar.
Esta manera de planificar contempla un aspecto organizativo sin duda necesario, ya que marca cuál va a ser el objeto específico de reflexión en cada momento del trabajo en el aula. Pero al mismo tiempo puede hacer perder de vista el hecho de que hay un conjunto importante de conceptos que desempeñan un papel fundamental en la adquisición del concepto de proporcionalidad, y que esos conceptos están siendo elaborados simultáneamente con la noción de proporcionalidad.
Efectivamente, pensar en relaciones de proporcionalidad directa nos puede remitir a situaciones como las siguientes:
– En la librería todos los artículos están rebajados un 20%.
– Cada 2 kg de fruta se obtiene 1,5 kg de mermelada.
– El tren marcha a 100km/h.
– El plano de la casa está hecho a una escala de 1:250.
– La presión del agua bajo la superficie del mar es directamente proporcional a la profundidad.
– Calcular cuántos paquetes de figuritas (todos iguales) es necesario comprar para tener 60 figuritas.
– Averiguar de qué material está hecho un cubo de 5 cm3 de volumen que pesa 1 kg.
Los diversos niveles de complejidad de cada una de las situaciones anteriores están dados, entre otras cosas, por los tipos de números en juego (naturales, enteros, racionales); la naturaleza de las magnitudes intervinientes (longitud, peso, área, volumen, peso específico, velocidad, presión); la conceptualización acerca de la medida; la variedad de contextos de utilización; los conceptos derivados de ciertos contextos de utilización (porcentaje, escala, velocidad, peso específico).
Es por eso que, al plantear el problema del aprendizaje de la proporcionalidad, es necesario tener en cuenta que la misma se inscribe en el campo de lo multiplicativo, que se trata de un proceso complejo en el que aparece una red de conceptos relacionados unos con otros, todos los cuales se van adquiriendo simultáneamente durante un período prolongado de tiempo. Es por eso también que es necesario pensar en aproximaciones sucesivas al concepto de proporcionalidad, cada una de las cuales va enriqueciendo su significado al tiempo que amplía la comprensión de los conceptos conectados. A continuación presentamos algunos problemas que pueden plantearse en los primero años del segundo ciclo.
- Paola colecciona figuritas. La siguiente tabla muestra la relación entre algunas cantidades de paquetes y la cantidad total de figuritas que obtiene. Completar la tabla, sabiendo que todos los paquetes traen la misma cantidad de figuritas.
| Cantidad de paquetes |
4 |
8 |
2 |
10 |
||
| Cantidad de figuritas |
20 |
100 |
120 |
- Un motor consume en 4 horas 24 litros de combustible. Completar la tabla que relaciona el tiempo de marcha del motor con la cantidad de combustible que utiliza, sabiendo que el gasto de combustible, por hora, es siempre el mismo.
|
Tiempo de funcionamiento (en horas) |
4 |
8 |
2 |
10 |
||
|
Combustible que consume (en litros) |
24 |
120 |
180 |
- En séptimo A, 4 de cada 7 alumnos concurren al viaje de egresados. En séptimo B concurren al viaje 5 de cada 8. ¿En cuál de los dos cursos es mayor la proporción de alumnos que concurren, respecto del total de alumnos de la clase?
- Don Francisco y don Tomás venden las figuritas que colecciona Paola. En el quiosco de don Francisco, el precio de 5 paquetes es de $ 3,5. En lo de don Tomás el importe de 8 paquetes asciende a $6. ¿En cuál de los dos quioscos es menor el precio de un paquete?
- Un jabón en polvo viene en paquetes de 500 gramos a $ 3,70 o en paquetes de 300 gramos a $ 2,10. ¿Cuál de los dos envases resulta más económico?
- Laura estuvo haciendo un plano para su departamento: una habitación, cocina, baño y un hall de entrada.
- a. Completar la siguiente tabla, sabiendo que con 1 cm va a representar 1 m (o sea con una escala de 1cm / m):
|
Medida real |
Medida sobre el plano (en cm) |
||
|
Habitación |
Largo |
4 |
……… |
|
Ancho |
3,50 |
……… |
|
|
Baño |
Lado |
1,50 |
……… |
|
Cocina |
Largo |
3 |
……… |
|
Ancho |
2,50 |
……… |
|
|
Hall |
Lado |
1 |
……… |
b. Dibuja un plano con las medidas de la tabla anterior.
c. Al fin se decidió por otra escala. El lado del baño quedó sobre el plano, de 3 cm. ¿Qué escala utilizó esta vez? ¿Por qué?
- Laura, Aníbal y Julieta se pusieron de acuerdo: al terminar la fiesta dividirían el resto de la torta en tres partes iguales: una para cada chico. Completa la siguiente tabla, que relaciona la fracción que recibirá cada chico con algunos posibles restos de torta:
|
Fracción de torta restante |
Fracción (con respecto a la torta original) para cada chico |
|
1/2 |
… |
|
1/3 |
… |
|
1/4 |
… |
|
… |
1/4 |
Para tener en cuenta:
– la diversidad de procedimientos en el aula, junto con el intercambio de los mismos entre los compañeros constituyen factores de progreso en el conocimiento. El alumno amplía su propia comprensión tanto cuando necesita encontrar palabras para explicar sus producciones, como cuando debe centrarse en el punto de vista de otro alumno;
– la utilización de uno u otro procedimiento por parte del alumno debiera atender a las características de la situación y a razones de economía;
– los problemas de regla de tres son problemas de proporcionalidad directa en los que se da un par de elementos que se relacionan y se pide hallar el correspondiente de otro elemento. No hay nada que justifique su tratamiento separado de la proporcionalidad;
– el docente puede propiciar o bloquear determinados procedimientos a partir de variar los datos de los problemas que propone.
Multiplicación con decimales
(Esta secuencia está propuesta por Graciela Chemello, Mónica Agrasar, Silvia Chara y Analía Crippa, a partir del Programa Matemática para Todos del nivel primario)
Para avanzar en la construcción de las operaciones con números decimales, en esta secuencia se propone que la resolución de problemas de lugar a la elaboración de estrategias de cálculo mental como las que se proponen hasta llegar, más adelante, a la reflexión sobre las propiedades de las operaciones, tomando la multiplicación como objeto.
Actividad 1: Librería Buenacompra
- Para comprar un diccionario de sinónimos, en la Librería Buenacompra, se ofrece un precio contado de $165,85. Mariela no cuenta con ese dinero y la vendedora le propone abonar un anticipo de $ 45 y 6 cuotas de $26,15. ¿Cuánto ahorra si paga al contado?
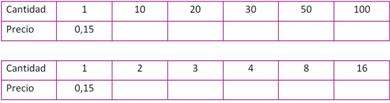
Ramiro fue a la misma librería y en el sector de fotocopiado sacó 20 fotocopias que costaban $ 0,15 cada una. Había un cartel que indicaba una oferta:
![]()
¿Cuál es el valor que se podría ahorrar con la oferta cuando se sacan 100 fotocopias?
- Gisela compró 5 lápices y pagó en total $ 7,5. Para averiguar el valor de cada lápiz se le ocurrió pensar que 10 tendrían que costar $15 y dice que cada lápiz cuesta $1,5. ¿Es correcto lo que pensó Gisela? ¿Por qué?
Tarea: Completar la tabla con el valor de distintas cantidades de fotocopias, sabiendo que no se hacen descuentos.
Actividad 2: El Juego de la Guerra con Cartas y un dado
Para jugar, júntense en grupos de cuatro compañeros reunidos de a 2 por equipo. Van a necesitar un mazo de 48 cartas con decimales como éstas (estas son 12 cartas y hay que tener cuatro de cada una), y un dado cuyo uno vale 10 (las otras caras siguen valiendo 2, 3, 4, 5, 6 respectivamente).
![]()
En cada ronda, se reparte una carta para cada equipo y, por turno, se tira el dado para obtener el producto entre la carta y el valor obtenido en el dado. El equipo que obtiene el mayor resultado, se queda con las cartas.
Si ambos equipos obtienen el mismo resultado, se juega una “guerra”: se coloca una nueva carta sobre la anterior y se vuelve a tirar el dado, repitiendo el procedimiento anterior. Gana el producto mayor.
Cuando se terminan las cartas del mazo, se cuentan las obtenidas durante las rondas por cada equipo y gana el que reunió más cantidad.
Tarea
Completá de modo que haya guerra
0,50 x …. = 0,25 x …
1,25 x …. = 0,25 x …..
1,50 x …. = 2,25 x ….
Actividad 3: Después del juego
I. Marcos dice que hay un montón de posibilidades de que haya “guerra”. Por ejemplo, carta 0,50 y dado 2 con carta 0,25 y dado 4; carta 1,50 y dado 2 con carta 0,75 y dado 4.
- Encontrá otros ejemplos.
- ¿Con otros valores del dado sucede algo similar? ¿Cuáles?
- ¿Con todas las cartas sucede esto?
II. Para hacer las multiplicaciones durante el juego, los grupos encontraron distintas estrategias.
Analizá los procedimientos que usaron algunos chicos para decidir, si son correctos y si lo son, cuál te parece más fácil:
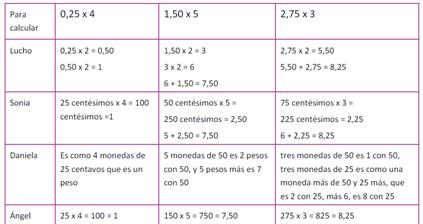
Tarea
Resolvé los siguientes cálculos (Nota para el docente: la idea es que los alumnos resuelvan estos cálculos sin usar el algoritmo de la multiplicación sino usando algunas de las estrategias anteriores).
0,75 x 20 = 0,75 x 40 = 0,75 x 80 =
1,75 x 20 = 1,75 x 40 = 1,75 x 80 =
2,75 x 20 = 2,75 x 40 = 2,75 x 80 =
Actividad 4: Con calculadora
Si en la calculadora se anota el número que aparece en la columna de la izquierda, ¿cómo se puede hacer para obtener el resultado que aparece en la columna de la derecha haciendo un solo cálculo?
- Registrá lo que pienses y comprobálo con la calculadora.
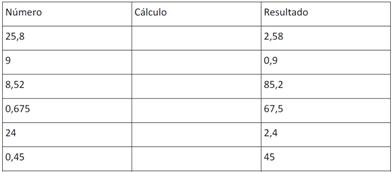
- Ángel dice que se puede completar la tabla usando multiplicaciones o divisiones. ¿Es cierto lo que dice? ¿Por qué?
- Resolvé (Nota para el docente: la idea es que los alumnos resuelvan estos cálculos sin usar el algoritmo de la multiplicación):
10 x 0,3 = 0,3 : 10 =
10 x 0,045 = 0,045 : 10 =
100 x 0,07 = 0,07 : 10 =
Tarea
- Sabiendo que 165 x 23 = 3795, calculá:
165 x 2,3 = 1,65 x 23 =
165 x 0,23 = 0,165 x 23 =
¿Qué es lo que tenés en cuenta para saber el resultado? - ¿Por cuánto hay que multiplicar o dividir 8,765 para que se transforme en …
0,8765
0,08765
87,65
876,5
Actividad 5: Multiplicar y dividir por 10, 100, 1000
- Completá la siguiente tabla:
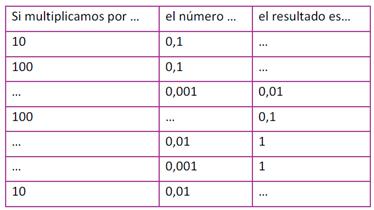
- Teniendo en cuenta los resultados de la tabla, resolvé:
10 x 0,3 = 10 x 0,15 =
10 x 0,045 = 100 x 0,9 =
100 x 0,07 = 100 x 0,806 = - Resolvé estos cálculos:
1 : 10 = 0,1 : 10 = 5,4 : 10 =
5,4 : 100 = 150 : 100 = 28 : 100 = - Escribí tres ejemplos de multiplicaciones y tres de divisiones de números decimales por 10,100, 1000.
Actividad 6: Yasi Berá
- El paraje Yasí Berá comienza a inundarse cuando el río alcanza los 6,7 metros de profundidad. Al iniciar la época de crecidas el río tiene 5 metros de profundidad y se estima que aproximadamente va a crecer entre 0,25 m y 0,40 m por día. Si se mantienen las condiciones, ¿en cuántos días se puede esperar, que comience a inundarse Yasí Berá?
- Para resolver el problema unos amigos decidieron averiguar el mínimo y el máximo de días que podría tardar en inundarse. ¿Cómo lo pueden haber averiguado?
- Otros compañeros hicieron el cálculo 0,65 : 2 y dijeron que se inundará en 5 días aproximadamente. ¿Es correcto? ¿Por qué?
- Marina hizo los siguientes cálculos
1,7 : 4 = 0,25 + 0,175 = 0,425
¿Es correcto? ¿A qué resultado habrá llegado?
Actividad 7: Distintas formas de resolver una cuenta
En 5° “D”, la Seño pidió a los chicos que reunidos en grupos, resolvieran 0,25 x 48. Estas son algunas tarjetas con las producciones.

- Explicá cada procedimiento.
- ¿Cómo resolverías vos el cálculo?
- Compará tu procedimiento con alguno de tus compañeros. Indicá qué tienen en común y en qué se diferencian.
- Resolvé 0,125 x 36 de dos maneras diferentes.
Tarea
- Resolvé
3,5 x 3= 0,25 x 5= 4,50 x 8=
0,02 x 40= 0,003 x 50= 0,008 x 80= - Pensá, sin hacer la cuenta, si
3,45 x 6 da más o menos que 20
3,75 x 4 3,50 x 4 y 3,25 x 4 dan más o menos que 15
Escribí cómo lo pensaste.
Actividad 8: Cuentas para corregir
I.
- Explicá en qué se confundió Laura al realizar esta cuenta
15,67
__x7__
10,969 - Un amigo no puede explicar qué hizo mal Laura pero sabe que el resultado no es correcto porque dice que 15 x 7 es más o menos 100. ¿Estás de acuerdo? ¿Por qué?
II. Martín hizo los siguientes cálculos.
0,4 x 4= 0,16
2,2 x 5 = 10,10
0,25 : 5 = 0,5
12,45 x 10 = 12,450
¿Se equivocó? ¿Por qué?
III. Cuando multiplicás un número natural por otro decimal, ¿cómo te podes dar cuenta que no te equivocaste al colocar la coma?
Actividad 9: ¿Vale o no vale?
Explicá si las siguientes afirmaciones valen siempre, a veces o nunca.
– Cuando se multiplica un número decimal por un número natural el producto es siempre mayor que el número natural.
– ¿Es lo mismo multiplicar por 0,1 que dividir por 10?
Escribí una regla que permita averiguar fácilmente el resultado de multiplicar o dividir por 10. Luego hacelo para 100 y para 1000.
Actividad 10: Mirar lo que aprendimos
- ¿Qué actividades te resultaron más fáciles?
- ¿Cuáles te costaron más? ¿Por qué pensás que te resultaron más difíciles?
- ¿Cómo haces para darte cuenta si el resultado de una multiplicación entre un número natural y un número decimal es razonable?
- Si un amigo te pregunta cómo se resuelven las multiplicaciones por decimales, ¿qué le dirías?
- ¿Tendrías que repasar algo más para poder resolver cuentas entre números naturales y números decimales?


